Die 13 bringts zum Laufen               see mixed english version

Die vorhergehenden Seiten behandelten eher das System der beiden großen Bessler-Räder. Die ersten, kleinen Räder waren etwas einfacher gebaut, vom Prinzip her aber gleich, ein Rad im Rad bzw. Unwuchtsystem im Rad.

Die einfachere Lösung dieser Räder eignet sich besser die geniale Erfindung Besslers zu erklären. Einfach ausgedrückt wird das Bessler-Rad angetrieben von einem im Inneren andauernd nach unten laufendes Rad, wie die bereits bekannte Abbildung zeigt. Der Drehpunkt liegt links vom Schwerpunkt, das Rad kippt also nach rechts und rollt nach unten. Die nachstehende Bildfolge zeigt wie dieses nach unten laufen durch ein resonantes Schwingen ersetzt wird. Man kann sich das so vorstellen: Das innere Rad läuft einen Zahn nach unten. Durch die Kopplung am rechten Rand gibt es Energie an das äußere Rad ab, mit der Energie des äußeren Rades schwingt es dann wieder nach oben und es geht von vorne los.

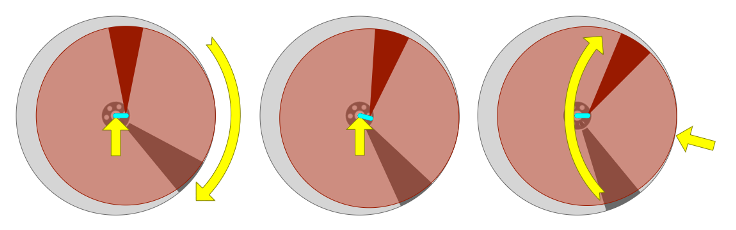Das Rad hat sich um einen Zahn weitergedreht, aber der nächste Zahn ist wieder auf der gleichen Höhe wie der vorhergehende Zahn. Und das kann dann ewig so weitergehen - eine perpetuierliche Bewegung nach Bessler.
Nur durch einen resonanten Energieaustausch zwischen innerem und äußerem Rad kann das Gesamtkunstwerk zum selbstlaufenden Rad werden.
Neben der Anordnung der Fluggewichte im Unwuchtsystem spielt auch das Geheimnis in der Achse (Getriebe mit Drehfeder) eine wichtige Rolle. Gewicht und Energie der Fluggewichte werden immer wieder zwischen den Rädern getauscht. Das Geheimnis in der Achse liefert die Synchronisation.

Vielleicht hat Bessler das gemeint in seiner Apologischen Poësie auf Seite 88:
   Der Geiz ist eine Wurzel böß' (ohne Energieaustausch geht es nicht)
   Ein Amboß krieget viele Stöß'. (der Amboss kommt gleich ins Spiel)

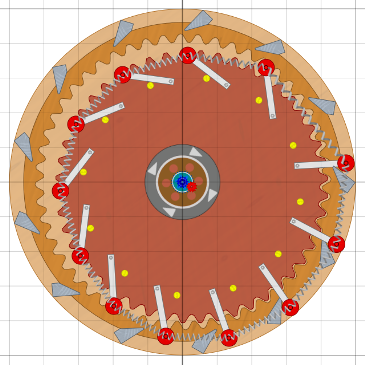Nachdem im besslerwheel-Forum wieder mal MT137 auftauchte, entwarf ich ein Unwuchtsystem mit 12 Fluggewichten und entsprechenden Zug-Riemen und integrierte es nach rechts versetzt in das größere äußere Rad. Da kam die Frage auf: Wie sollte der Energieaustausch stattfinden?
Allein über die Achse (Getriebe) oder auch am Umfang?
Zwölf Ambosse am Umfang (Bild oben links), das passte nicht, die Gewichte liegen nicht lange genug auf.
Wie wärs mit 13? (rechts) ... Treffer, ideal, super! Jetzt drehen sie das äußere Rad von 3 Uhr bis 5 Uhr. Auch der Versatz der beiden Rad-Wellen ist damit definiert, nicht zu groß und auch nicht zu klein, irgendwie optimal. Sofort kam mir auch die Maya-Weisheit in den Kopf: „ ... die dreizehn bringt es in Bewegung!”

Die Zähnezahl des äußeren Rades sollte also ein Vielfaches von 13 sein. Jetzt weiß ich warum der Holzschnitt des Merseburg-Rades 117 Montagezapfen am Umfang zeigt: 117 = 13 x 9.

Natürlich gibt es auch wieder eine Algodoo-Szene zum Simulieren und Optimieren. Bei mir läuft es bei ca.7 U/min am besten und benötigt dabei unter 1 Watt Motorleistung. Damit es wie bei Bessler mit 40 U/min laufen kann, muss noch die passende Drehfeder eingebaut und auf ca. 10 Hz abgestimmt werden. Damit habe ich noch meine Probleme. Dass die Szene nicht „rund läuft” liegt meiner Meinung nach an den Zahnrädern im Zentrum. Evtl. gibt es da einen Fehler in Algodoo beim Erstellen von Zahnrädern einer bestimmten Größe.

Download meiner Szene hier oder durch klicken auf das Bild.

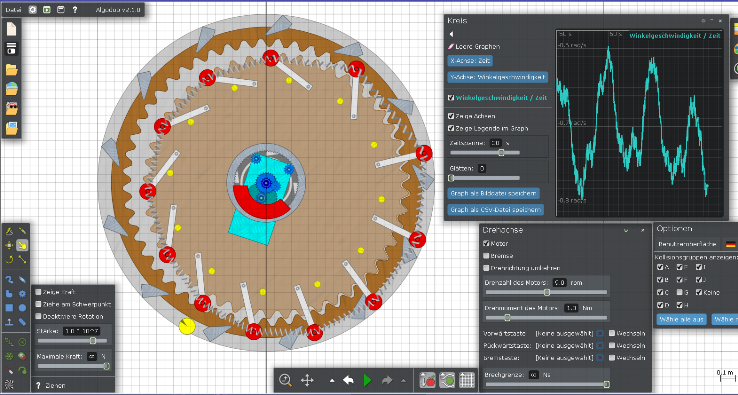
Wenn ich die Szene betrachte, habe ich immer eine Assoziation zu MT13, siehe Seite Impulsaustausch.
Da steht die 13 sogar im Titel.
Ich habe auch noch weiter gesucht, wo Bessler evtl. dieses System 12:13 versteckt oder codiert haben könnte. Und ich bin fündig geworden, bei MT55.

Schon immer habe ich mich gewundert, warum das Zahnrad rechts oben 49 Zähne hat. Das muss doch irgendetwas bedeuten. Jetzt weiß ich es. Wie wir oben gesehen haben, gibt es auf dem Unwucht-Rad zwölf Fluggewichte, das äußere Rad hat dafür aber 13 Aufrastungen (Ambosse). Eine 12:13-Übersetzung wird also auch beim Getriebe im Zentrum nötig. Und genau diese wird in MT55 dargestellt. Das linke Zahnrad hat 12 Zähne, das rechte hat 4+9=13 Zähne, codiert wie man es von Bessler erwartet. Weitere Aspekte deuten auf diese Interpretation: - die zwei Zahnräder sind oben waagrecht dargestellt - unten sind die Zahnräder ähnlich groß - die zwei Zahnräder verkoppeln zwei Wellen - es gibt einen Energieaustausch zwischen den Wellen Wie man aus diesem Beispiel sieht macht es wenig Sinn den Aufbau des Bessler-Rades aus seinen Maschinentractaten herauslesen zu wollen. Es hilft aber sehr wohl, wenn man nach vielem Nachdenken und Ausprobieren eigene Lösungen gefunden hat und diese dann bei Bessler in codierter Form wiederfindet.

nächste Seite