Der Drehpunkt

So jetzt kommen wir zum zweiten Geheimnis in der Achse, zum eigentlichen Bessler-Geheimnis, der Verschiebung des virtuellen Drehpunktes. Beim ersten Bild sehen wir, dass der Drehpunkt (gelber Pfeil) nicht im Zentrum des Rades liegt. Das Rad wird sich drehen, aber leider auch nach unten wegkippen. Ein stetiges Weiterdrehen erreichen wir indem wir dem Rad immer wieder einen neuen Drehpunkt anbieten (mittleres Bild). Hier ist die logische Folge, dass das Rad bergab rollt - und irgendwann unten ist.
Und jetzt kommt der Motus ins Spiel. Hat Bessler damit die perpetuierliche Bewegung erreicht?

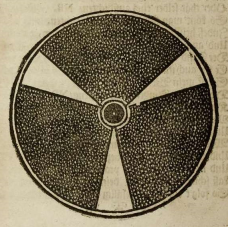Hat Bessler es geschafft, dass das Rad einen Zahn hinunterrollt, um im mittleren Bild zu bleiben, dann aber wieder auf die ursprüngliche Höhe zurückgehoben wird, um denselben „Zahn” immer wieder hinunter rollen zu können?

Ja, Bessler hat es geschafft ! Das ist sein Prinzip, sein Geheimnis.

Wer meine bisherigen Seiten gelesen hat, weiß, dass ich ein Fan des Motus als Getriebe bin. Nachdem ich den Motus mit drei Feldern nicht richtig unterbringen konnte, habe ich es mal mit vier Feldern probiert - ich bin begeistert. Mit dem Getriebe-Motus haben wir automatisch einen Wellen-Versatz, jetzt müssen wir nur dafür sorgen, dass das Antriebsrad nicht einfach nach unten kippt. Wir brauchen ein Gegengewicht, einen Doppel-Oktav-Pendel. Dieser muss pro Radumdrehung vier volle Schwingungen ausführen.

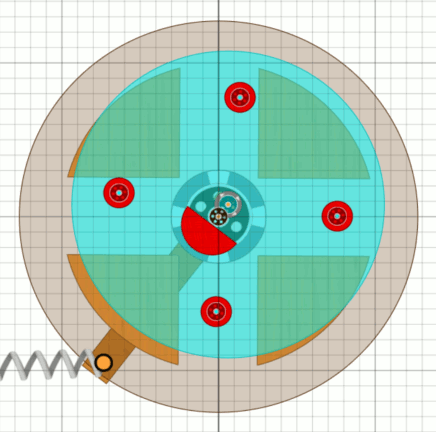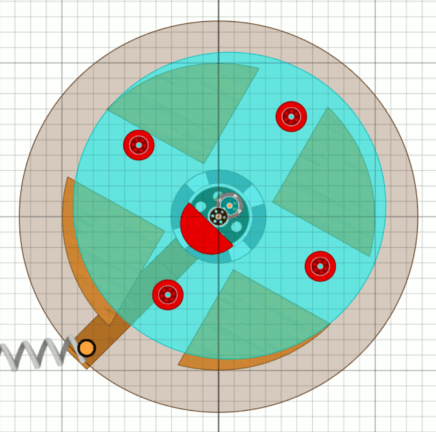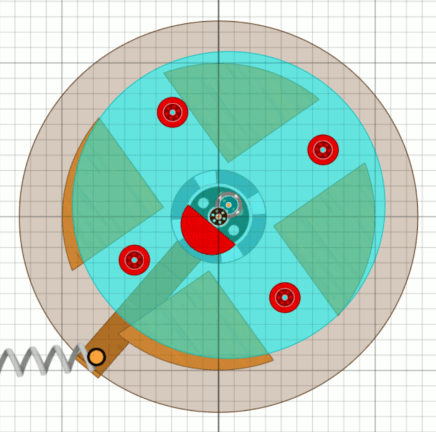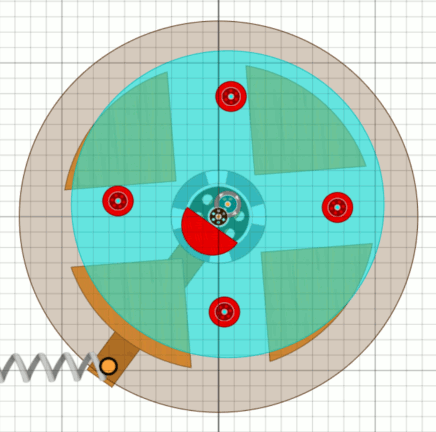Das oben beschriebene hinunter rollende Rad ist hier die türkise Scheibe, später das Unwuchtsystem oder Unwucht-Kreuz. Das Gegengewicht, der Doppel-Oktav-Pendel ist der rote Halbkreis, wegen der sehr kurzen Schwingungsdauer ein sehr kurzer Pendel. Die in der Animation sichtbare Feder wird nur noch benötigt, weil das Rad ja nicht vollständig ist. Immer wenn ein Zapfen (Kugellager) von unten auf den Motus trifft, wird der Motus (Bessler-Rad) getrieben, die Exzenterwelle weicht nach unten aus und das Gegengewicht geht nach oben. An der Exzenterwelle hängen dann auch die zwei Pendel, die den Umschwung der Fluggewichte auslösen. Ihr Schwingen unterstützt zusätzlich die Bewegung des Gegengewichts. Beim Rückschwung des Gegengewichts wird das Unwucht-Kreuz dann wieder auf die Ausgangsstellung zurück gehoben.

Hier gibt es die Algodoo-Datei zum download. Und mit dem folgenden Bild will ich einen Erklärungsversuch wagen, warum sich dabei der Drehpunkt des Unwucht-Kreuzes verschiebt.

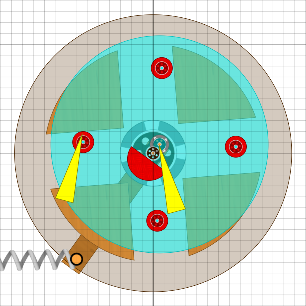Die Exzenterwelle ist der Drehpunkt des Unwuchtsystems (rechter gelber Pfeil). Trifft aber ein Zapfen des Unwucht-systems von unten auf den Motus (linker gelber Pfeil), so teilt sich der Drehimpuls auf. Ein Teilimpuls beschleunigt den Motus, ein weiterer Teilimpuls lässt das Unwuchtsystem etwas nach rechts unten kippen. Die Unwucht kippt deshalb nach unten, weil ja der Drehimpuls konstant bleiben muss, auf der linken Seite das Hochdrehen aber gebremst wird. Es gibt also kurzzeitig einen virtuellen Drehpunkt zwischen den gelben Pfeilen, er liegt nicht genau dazwischen, sondern in der Nähe des rechten Pfeils. Damit haben wir die gewünschte Drehpunktverschiebung erreicht - q.e.d. Das Prinzip ist erkannt, jetzt geht es an die Konstruktion.

nächste Seite