Der Motus als Getriebe

Die letzten zwei Seiten haben wichtige Merkmale eines Bessler-Rades aufgezeigt. Meine Lösung zum Video von Per-Henrik gibt einen Hinweis auf eine exzentrisch gehaltene Masse im Rad, evtl. ein Rad im Rad-System. Das Beispiel zum Impulsaustausch gibt Hinweise auf Pendel mit Ratschen. Gleichzeitig wissen wir, dass die Winkelgeschwindigkeit des Pendels größer als die des Rades sein muss, sonst kommt keine Impuls- oder Energieübertragung zustande.
Bekommen wir all das durch einen Motus?

download Algodoo-Szene

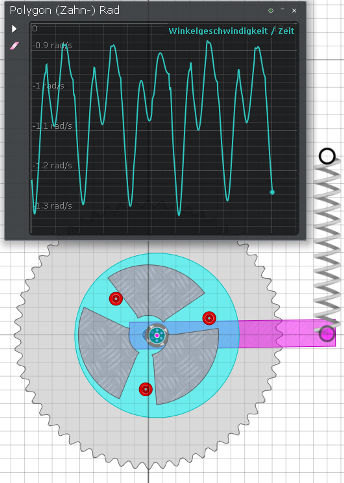
Hier eine kleine Test-Anordnung mit einem Motus. Das Zahnrad hat dabei keine Funktion, es stellt nur das Rad dar. Mit dem Rad fest verbunden sind die Motus-Kurven (Kuchenstücke), und das Rad wird definiert gebremst. Von der Achse des Rades geht ein Balken nach rechts, der von einer Feder waagrecht gehalten wird. Auf diesem Balken sitzt nun das Zentrum der türkisen Scheibe mit den Mitnehmerzapfen (kleine rote Kugellager), die in die Motus-Kurven eingreifen. Diese türkise Scheibe ist leicht nach rechts versetzt und wird in dieser Szene angetrieben mit 10 U/min. Immer wenn ein Mitnehmer zwischen 10- und 11-Uhr auf ein Kurve aufsetzt steigt die Winkelgeschwindigkeit des Rades abrupt um ca. 30 Prozent. Man kann den Motus also als Getriebe betrachten das eine konstante Drehbewegung umsetzt in eine schnelle Beschleunigung mit anschließender Verzögerung, fest definiert und periodisch. Auch der schwingende violette Balken hat seine Funktion: Je nach Anstellwinkel greifen die Zapfen schon bei 10-Uhr oder erst bei 11-Uhr in die Motus-Kurven ein. Außerdem kann der nachgebende und dann zurückfedernde Balken den Eingriff harmo- nisieren und verlängern. Da es aber im Bessler-Rad für die Feder keinen festen Aufhängungspunkt gibt, wird Bessler an der Stelle wohl einen Oktav-Pendel eingesetzt haben, also einen Pendel mit doppelter Frequenz als Gegengewicht zu den ausser der Mitte aufgehängten Ratschenpendeln.

Bessler hat uns das Bild des Motus an exponierter Stelle in seiner Schrift hinterlassen.
Der Motus ist wohl die Verbindung von innerem und äusserem System und gleichzeitig die Regelung.
Aber wie hat er das gemacht?

Wir müssen es herausfinden, durch Versuch und Irrtum!

nächste Seite