Das Prinzip - kontrollierte Resonanz

Timo G. hat immer wieder von kontrollierter Resonanz gesprochen, aber ich konnte mir einfach keinen Reim darauf machen. Jetzt plötzlich war alles klar. Drei Aspekte müssen in Resonanz gebracht werden, damit das Rad sich aus sich selbst heraus drehen kann:

- die Drehzahl des Rads (U/min)
- die Schwingungsdauer der Federarme (1 x pro Umdrehung)
- die Bewegung der Arbeitsmassen nach außen/innen (1 x pro Umdrehung)

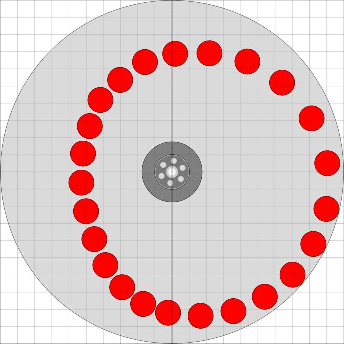
Gehen wir der Einfachheit mal davon aus, dass die Arbeitsmassen einfach auf den Federarmen verschoben werden können - nach außen und nach innen - dann würde der Ablauf in etwa so aussehen (Animation links).
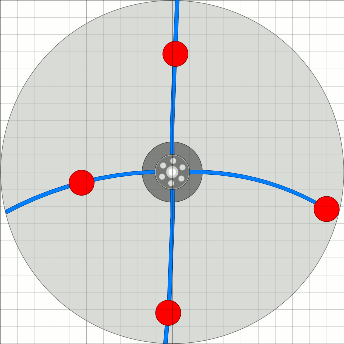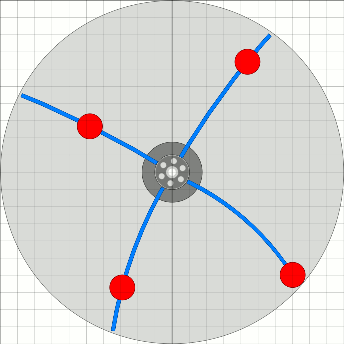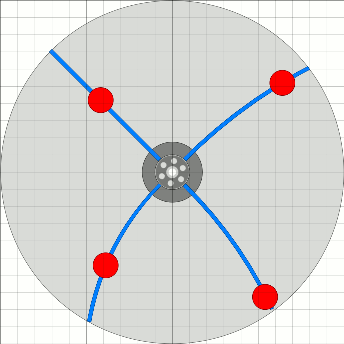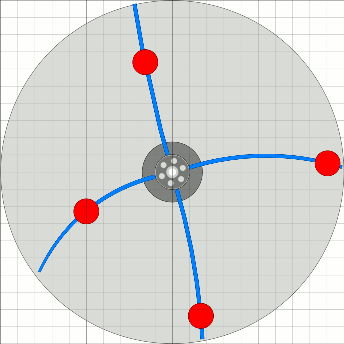
Im Bild rechts sind die Positionen der Arbeitsmassen im Abstand von je 15 Grad Raddrehung dargestellt.


Anhand von zwei Teilbildern im 45 Grad-Abstand können nun einige Details dargestellt werden. Interessant zu betrachten wird sein: das Drehmoment verursacht durch die Gewichtskraft einer Arbeitsmasse als auch das Drehmoment verursacht aus der kinetischen Energie der Arbeitsmasse am Federpendel. Dazu kommt noch der Pirouetteneffekt beim Aus- und Einschwingen der Arbeitsmassen sowie die Schwankungen der Fliehkraft.

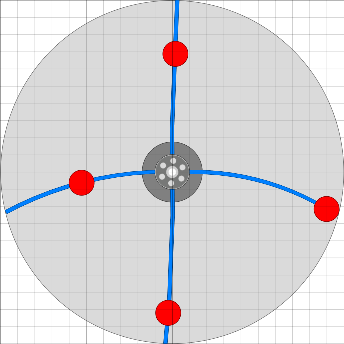Die Abbildung links zeigt das Rad bei Position 0 Grad (des Federarm-Kreuzes). Das Drehmoment des rechten Arms auf die Radnabe ist in zweifacher Hinsicht gerade maximal. Das Gewicht ist außen und der Arm steht fast rechtwinklig zur Schwerkraft, also maximales Dreh- moment zur Beschleunigung des Rades. Gleichzeitig pendelt die Arbeitsmasse in den Federarm hinein, die kinetische Energie biegt die Feder und bewirkt ein zusätzliches Drehmoment auf die Radnabe. Auf der linken Seite ist das Gesamtdrehmoment kleiner da das Gewicht näher am Drehpunkt ist. Zu betrachten ist aber noch das Drehmoment, das verlorengeht, weil ja die Arbeitsmasse in Richtung Welle gebracht, also angehoben werden muss. Das alles zu berechnen ist mir etwas zu hoch, aber ich sehe da noch den Pirouetten- Effekt, der beim Heranziehen der Masse eine Beschleunigung ergeben sollte.

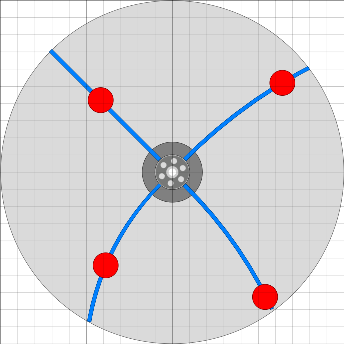Während beim 0 Grad-Bild unten die Einwärtsbewegung gerade beginnt und die Auswärtsbewegung oben fast abgeschlossen ist, sind diese Aktionen beim 45 Grad-Bild mitten drin. Was aber ist jetzt links unten besonders? Die Fliehkraft hat gerade ein Minimum! Durch die Federarme ist nämlich die Winkelge- schwindigkeit der Arbeitsmassen nicht gleich der Winkelgeschwindigkeit des Rades, sondern mal größer und mal kleiner (siehe Abstandsvariation der Arbeitsmassen im Bild ganz oben rechts). Hier unten hat sie ein Minimum, somit hat auch die Fliehkraft ein Minimum und es braucht weniger Energie zum Anheben der Masse. Ganz anders links oben: Die Winkelgeschwindigkeit der Arbeitsmasse steigt an und schleudert die Masse gleichsam nach außen. Bessler würde sagen: „ ... wie 's soll!”

Was wir jetzt aber noch brauchen um einen Prototypen bauen zu können ist ein Mechanismus zum Verschieben der Arbeitsmassen. Hier habe ich bis jetzt drei aussichtsreiche Mechaniken entwickelt, die im Folgenden dargestellt werden. Bessler hat hier wohl auch zwei verschiedene Systeme angewandt. Die Abroll-Version eher in den ersten zwei, eine andere in den letzten beiden Rädern.

nächste Seite