Die Software-Ratsche

Wie schon dargelegt, spielt im inneren System des Bessler-Rads die Ratsche eine bedeutende Rolle. Nun kann man eine Ratsche in Algodoo zwar irgendwie nachbauen, sie wird aber in der Regel zu groß, braucht viel Rechenzeit und funktioniert auch nicht verlässlich. So habe ich im Algodoo-Forum gesucht, wie man das besser machen kann. Und tatsächlich, es gibt da eine „Software-Lösung” in der Script-Sprache.
Mit der Script-Sprache (Thyme) kann man einzelne Objekte während der Simulation beeinflussen, z.B. kann die Farbe, die Größe oder die Drehzahl geändert werden. Gesteuert wird das durch sog. „Events” wie Zusammen-stoßen oder auch das Erreichen einer bestimmten Winkelstellung.

Zum Einstieg hier zwei Beispiele zum Zahnrad-System.
Hier ist noch keine Ratsche im Spiel, sondern nur eine Blockade abhängig von der Winkelstellung eines Objekts.

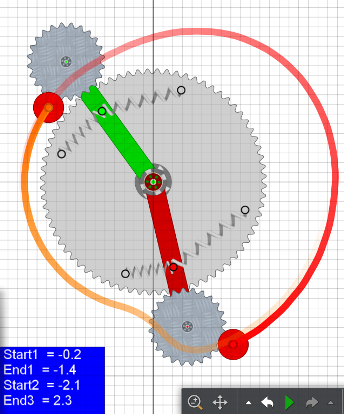	Wie schon früher erwähnt, hat das Zahnrad-System den Nachteil, dass der Satellit sich während des Abwärts-schwungs zu früh einzudrehen beginnt. Die Feder entspannt sich zu früh und so bleibt zu wenig Feder-kraft, wenn dann das Einschwingen stattfinden soll. Mit einer kleinen Script-Lösung kann man den Arm jetzt kurz blockieren und später wieder freigeben. Das passiert ab Winkelstellung Start1 = -0.2 (im Bogenmaß) bis End1 = -1.4. Gleichzeitig kann man eine Farb- änderung vorgeben, hier rot = blockiert, grün = frei. Wie die Simulation zeigt, kann man die notwendige Antriebsleistung damit auf ein Minimum reduzieren, hier bis 0.1Nm, was weniger als 0,2 Watt entspricht. In der Realität braucht man allerdings eine Kupplung, die wenig Energie verbraucht. Das sollte aber machbar sein, wenn man erst mal weiß wie die Funktion sein muss. Wer das selbst ausprobieren will kann sich sowohl die Algodoo-Szene sowie eine Word-Datei herunterladen in der die notwendige Script-Programmierung erklärt ist. Die Word-Datei braucht man nur, wenn man die Start- und End-Winkel verändern will. download Algodoo-Szene -- download Word-Datei
Und fast so einfach geht es mit drei Satelliten:
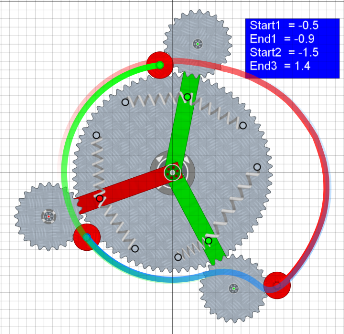	Da die einzelnen Drehpunkte der Hebelarme im Zentrum nur schwer zu fassen sind, habe ich hier die Achse der Satelliten blockiert. Neben der Farbänderung der Arme kann man die Blockierung jetzt auch direkt an der Achse der Satelliten sehen. Wie die Simulation zeigt, kann man die notwendige Antriebsleistung hier aber nicht so weit reduzieren. Ich schaffe als Minimum gerade mal 0.75Nm, was bei dieser Drehzahl ca. 1,1 Watt entspricht. Zum Spielen und Optimieren stelle ich auch hier wieder die Algodoo-Szene sowie die zugehörige Word-Datei zur Verfügung. Zum Ändern der Parameter (Start und End) kopiere ich sie in der Word-Datei, gehe dann ins Algodoo-Fenster, rufe mit F10 die Konsole auf, lege sie dort ab und aktiviere sie durch Enter. Dann nur noch mit Esc die Konsole verlassen. download Algodoo-Szene -- download Word-Datei
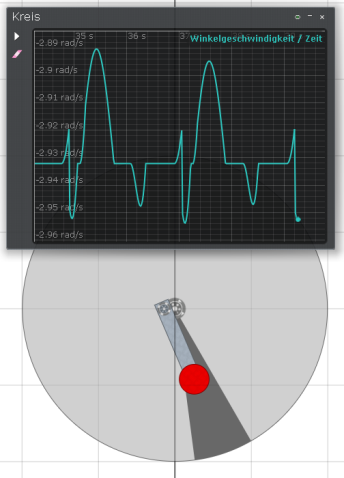
Jetzt kommt die Ratschenfunktion:
	Werden in Algodoo zwei Objekte mit einer Drehachse verbunden, so wird zwischen ihnen ein Bezug hergestellt. Das Objekt mit der Achse ist geom0. Das darunterliegende Objekt ist geom1. Bei der Software-Ratsche wird einfach die Winkelgeschwindigkeit der beiden verglichen und entsprechend die Variable autobrake auf „true” oder „false” gesetzt. Mit motorTorque wird die Kraft der Kupplung eingestellt. Die Programmzeilen und Hinweise sind wieder in einer Word-Datei zu finden. Diese Szene hat mir wieder gezeigt wie gut die Algodoo-Simulation die Realität abbildet. Bei einem realen Aufbau eines Rades mit exzentrisch aufgehängtem Pendel bestehend aus einem Ratschenschlüssel und einem 300g-Gewicht bekam ich das gleiche Ergebnis, das ich vorerst nicht verstehen konnte: Der Eingriffspunkt der Ratsche im Resonanzpunkt (beim ungebremsten Rad) war ebenfalls bei ca. 11 Uhr. Simulieren lohnt sich also, wenn man weiß, was man tut. Hier wieder die Dateien: download Algodoo-Szene -- download Word-Datei

Für den interessierten Besslerfreund noch ein Hinweis:
Die exzentrisch aufgehängte Ratsche war wohl einer der Tricks von Bessler bei seinen ersten Rädern, siehe MT51. Bei einem resonant abgestimmten System aus Rad und zentrischem Pendel kann der Pendel nämlich nie seine Energie an das Rad abgeben, da seine Winkelgeschwindigkeit im Maximum der des Rades entspricht. Beim exzentrischen Pendel ist das anders. Da muss man eigentlich nur noch dafür sorgen, dass der Eingriff etwa bei 3 oder 4 Uhr erfolgt und der Pendel danach wieder angehoben wird.

nächste Seite