... zwei und zwei

„Der sind nun immer zwey und zwey/
Nimmt ein Ding äusserlich die Stelle/
So fährt das andre an die Welle/”       ... so schreibt Bessler in AP 81.

Nachdem der Antrieb der Fluggewichte jetzt prinzipiell geklärt ist, geht es nun an die Ausarbeitung der Mechanik, insbesondere der großen Übersetzung.

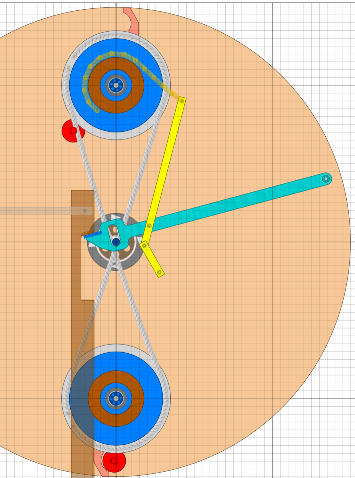
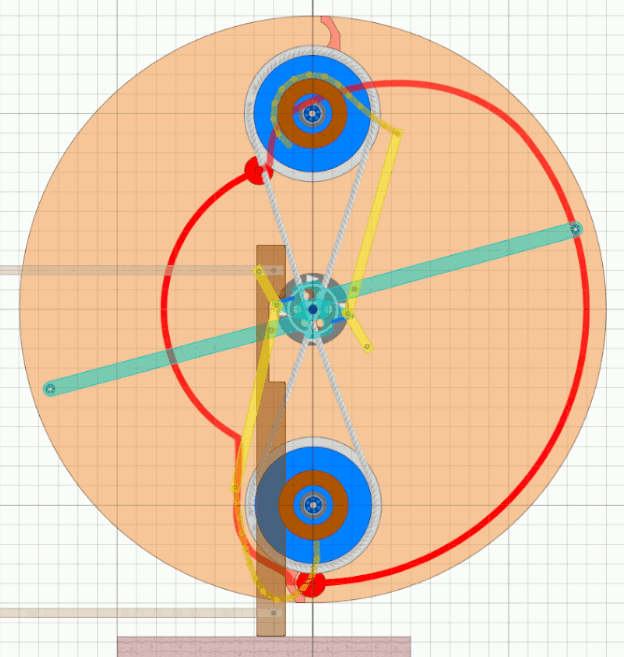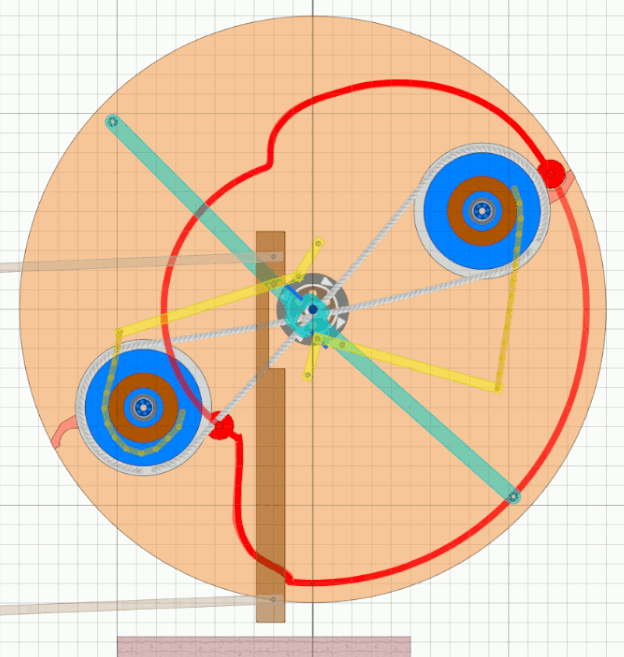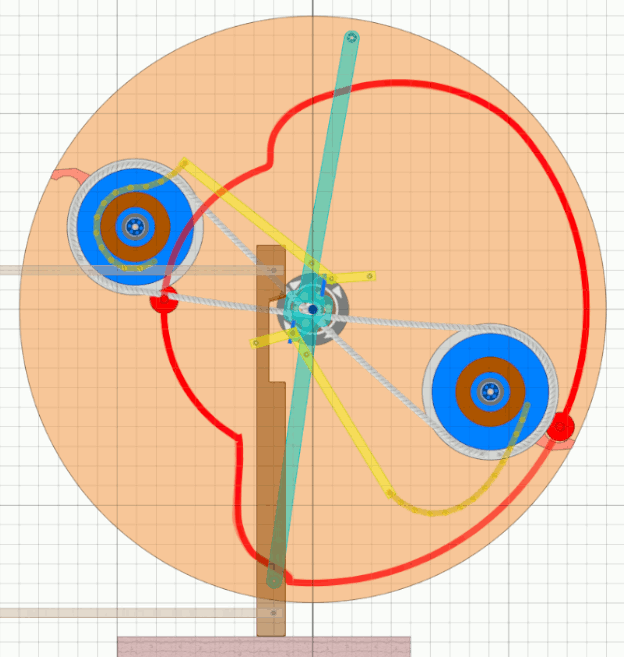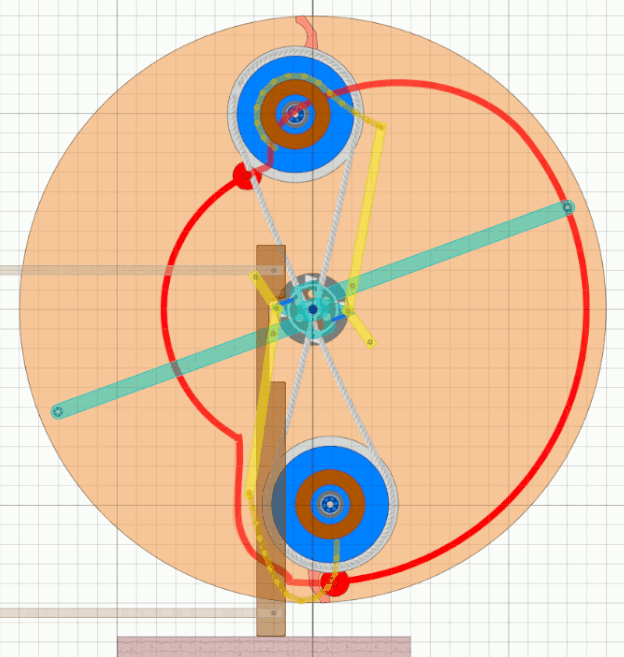
Die Übersetzung erfolgt hier durch die gelben Hebel.    Der türkise Hebel kann sich nur geringfügig in seinem    Langloch bewegen. Im Bild ist das obere Fluggewicht    innen und die gelbe Mechanik (Hebel und Seil)    hält den türkisen Hebel oben.    Wenn jetzt der Stampfer eingreift, so wird der türkise    Hebel nach unten gedrückt, der gelbe Hebel schwenkt    nach rechts und dreht per Seilzug das Fluggewicht    nach aussen.    Die zwei gelben Hebel stellen im Prinzip die Spar-    Ausführung eines Scheren-Mechanismus dar.    Bis auf den vorher mit A bezeichneten Drehpunkt    wirken alle auftretenden Kräfte beschleunigend    auf das Rad.        Anfangs müssen sich beide Fluggewichte in Bewegung    setzen und sogar angehoben werden. Genau da liefert    der Stampf-Mechnismus die größte Kraft. In der    Mitte der Schwingbewegung sinkt der Kraftbedarf,    da das untere Gewicht wegen des Pirouetteneffekts    relativ leicht einschwingt und beim oberen schon die    Fliehkraft wirkt, der Stampfer fängt an sich zu heben.    Dann aber steigt der Kraftbedarf wieder, wenn das    obere Fluggewicht aussen eigentlich langsamer    werden will, aber schneller werden muss.    Hier bleibt der Stampfer noch aktiv bis das    Fluggewicht seine Endposition erreicht hat.

Wie schon von früheren Simulationen bekannt hat Algodoo Probleme mit solchen Aufgaben.
Die Gif-Animation konnte nur erstellt werden bei sehr langsamer Drehzahl und minimierten Massen.
Die zur Animation verwendete Algodoo-Szene kann hier herunter geladen werden.

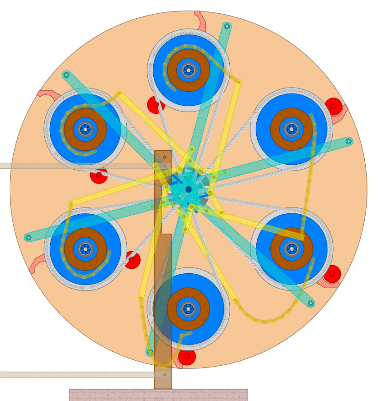
Die ersten zwei Räder hatten drei Stampfer    und damit wohl sechs Fluggewichte.    Die Gewichte bei 6-Uhr und 12-Uhr stehen hier    vor dem Ein- bzw. Ausschwingen.    Man kann sehen, dass die Gewichte bei 2-Uhr    und bei 4-Uhr eine Unwucht und damit ein    Drehmoment in Drehrichtung erzeugen.        Nach den vorangegangenen Überlegungen    kommt die Kraft zum Ein- und Ausschwingen    zum Großteil aus der Reaktionskraft    bei der Stampferhebung.    Die Unwucht (2- und 4-Uhr) muss also nur um    ca. 20 bis 30 % mehr Drehmoment erzeugen als    zur reinen Stampferhebung notwendig wäre.        Im Prinzip also nur noch eine Optimierungs-    Aufgabe sowie das Unterbringen    der Zapfenmechanik in der Achse.

Die Zapfenmechanik in der Achse sieht anfangs schwieriger aus als sie dann eigentlich ist, wenn man sie dreidimensional angeht. Man kann den Drehpunkt A sogar so in die Achse verlegen, dass er keinerlei rückwärts gerichtetes Moment mehr erzeugt - MT69 läßt grüßen.
Es gilt also nur starre und verwindungsfreie Materialien zu finden und die Aufhängungs- bzw. Drehpunkte an den richtigen Stellen zu plazieren. Mit der heutigen Technik ist das sicher kein Problem, in der Zeit Besslers jedoch eine Herausforderung und absolut bewundernswerte Leistung.

nächste Seite: die ersten Räder