Die Satelliten werden wieder vom Motus (3 Reibrad-Flügel) angetrieben wie bei den ersten Rädern. Die Mechanik dazu ist aber eine ganz andere. Der Motus dreht hier schneller und ccw. Das lässt sich sehr leicht aus der Raddrehung ableiten. Die Drehgeschwindigkeit muss aber vom Stampfwerk moduliert werden, und da ist bis jetzt noch vieles unklar.

Beim Stampfwerk gibt es nämlich eine Kuriosität. Läuft das Rad wie gewohnt im Uhrzeigersinn cw, so ist alles normal. Das Stampfwerk dreht sich in die gleiche Richtung wie das Rad, auch cw. Läuft das Rad aber gegen den Uhrzeigersinn ccw, dann muss das Stampfwerk trotzdem cw laufen, sonst würde es blockieren. Diese Umschaltung muss beim Starten des Rades automatisch erfolgen.
Es ist also nicht so, dass das Rad mit dem Stampfwerk nur cw laufen konnte und dann wenn es rechts- und linksherum zum Einsatz kommen sollte, das Stampfwerk einfach weggelassen wurde. Das Stampfwerk ist ja immerhin ein integraler Bestandteil des Bessler-Rades.

Auch die Weiterleitung des Stampferimpulses muss anders sein als bei den ersten Rädern. Während dort alle 60° ein Stampfer gehoben wurde und Zeit war in der sich die Achse zurückdrehen konnte, sind es jetzt nur 45° und diese ganze Zeit ist der Stampfer im Eingriff. Es muss also ein ganz anderer Mechanismus vorliegen oder die Achse ist zweigeteilt, so dass pro Hälfte 90° für einen Zapfen Zeit war (15° Torsion, 45° Unwucht bedienen, 30° Achshälfte wieder auf Anfangsposition).

Im Stich vom 3. Rad gibt es dafür keinen Anhaltspunkt, beim 4. Rad aber schon. Das 3. Rad lief ja im Leerlauf mit ca. 40 U/min, da waren vier Stampfer wohl notwendig um die 8 Impulse pro Umdrehung zu erzeugen. Die Stampfer mussten ja wieder am Boden stehen, wenn der nächste Eingriff erfolgte. Das 4. Rad lief im Leerlauf nur noch mit 26 U/min, da kam Bessler dann mit zwei Stampfern aus, von denen jeder vier Mal pro Umdrehung angehoben wurde. Es waren also zwei Zapfen-Kreuze an der Achse, um 45° versetzt, wie oben vermutet.
Hier nur am Rande bemerkt: Beim 4. Rad lief die Achse entgegengesetzt zu der vom 3. Rad.

Das Geheimnis in der Achse

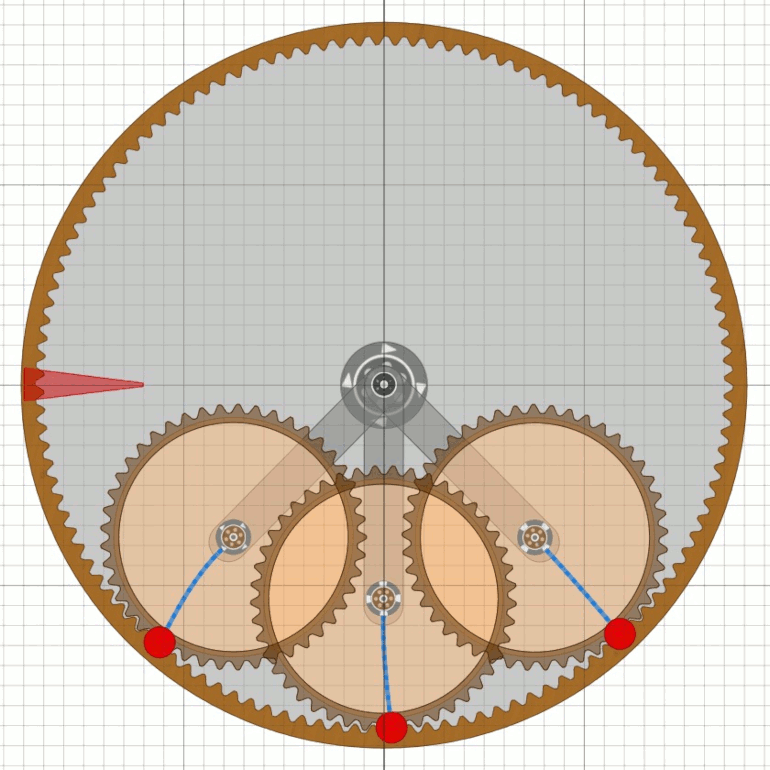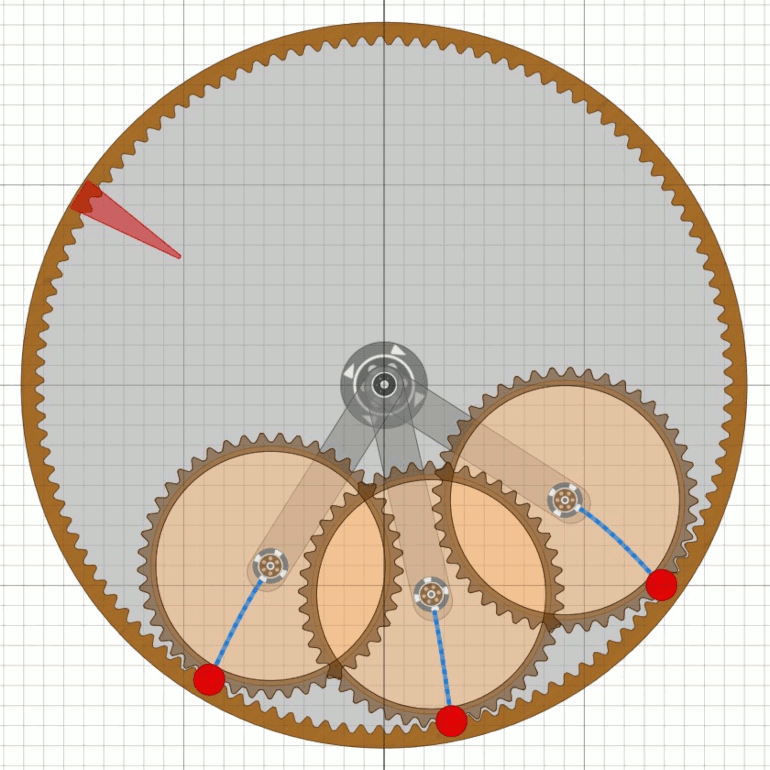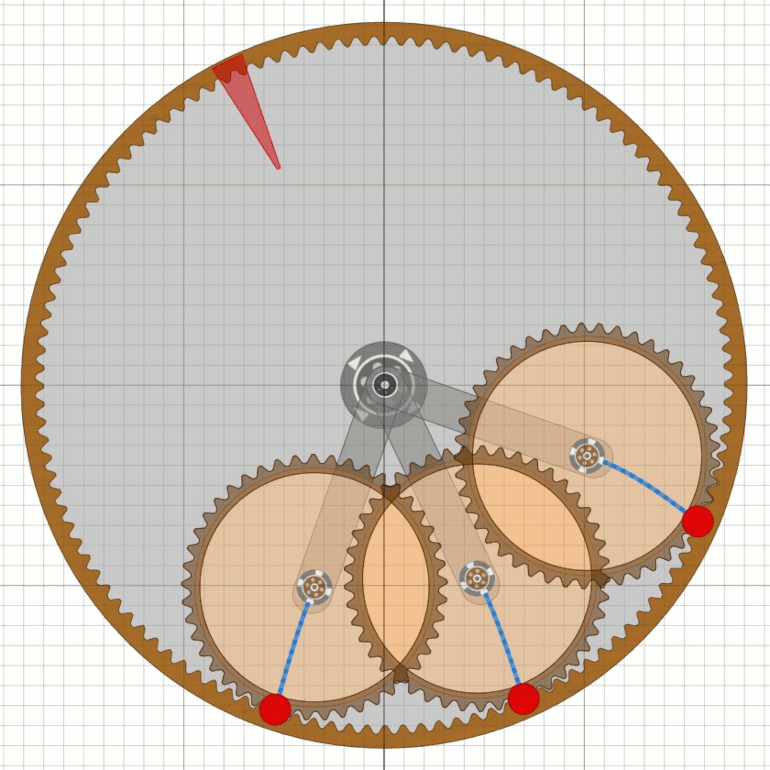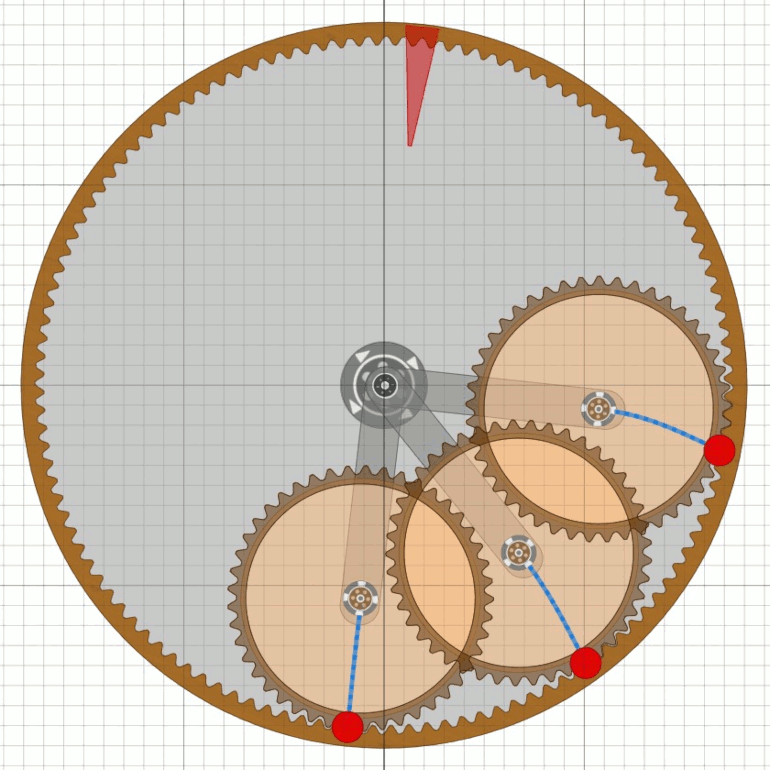
Das Geheimnis in der Achse der bidirektionalen Räder ist noch nicht gelöst. Ich will hier aber den Startvorgang kurz darstellen, damit man daraus evtl. mal eine geeignete Mechanik ableiten kann. Wir beginnen also mit dem Rad im Stillstand, siehe unten, und drehen das Rad langsam cw. Jetzt nehmen wir an, dass ein Motus-Flügel am linken Satelliten anliegt und diesen nach rechts wegdreht. Dadurch geht auch das Fluggewicht nach oben. Solange das Fluggewicht seine höchste Position nicht erreicht hat, ist der Vorgang reversibel, d.h. das Rad wird sich zurückdrehen, wenn wir es loslassen (Bericht von Willem Jacob `sGravesande).
Kommt das Fluggewicht aber über den oberen Totpunkt hinaus, so startet das Rad und erreicht innerhalb einer Umdrehung seine Nenndrehzahl.

Und das sagt uns Bessler wohl im Gründlichen Bericht auf Seite 16:
„..., so bald nur ein einziges von denen innwendig in dem Cörper des Kunst=Rades verborgenen Gewichten zu fallen angefangen/ die Machine nach und nach/ und ohngefehr in einer Umwendung von sich selbst in solchen starken Lauff gekommen/ und in ihrer egalite darinne verharret/ biß selbige mit aller force wieder aufgehalten worden;”.

Der Motus dreht sich hier 8/3-mal so schnell wie das Rad und zwar in entgegengesetzter Richtung.
Das Getriebe ist sogar einfacher als bei den ersten Rädern.
Vom äusseren Zahnkranz ausgehend könnte man die gewünschte Drehzahl mit zwei Zahnrädern ableiten.
Zwei Aspekte sprechen aber dagegen:
Das zentrale Zahnrad müsste 45 Zähne haben und das Zwischenzahnrad 37,5 - oha, das geht nicht.
Als zweiter Punkt spricht dagegen, dass wir ja wieder ein Steuerpendel brauchen, dieses wäre hier viel zu lang und hätte damit eine viel zu große Zeitkonstante (Steuerpendel = Träger des Zwischenzahnrads).
Wir brauchen also einen kleineren zusätzlichen Zahnkranz näher an der Welle.

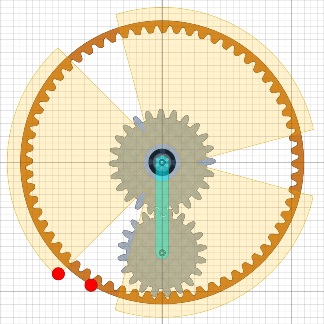Der kleinere Zahnkranz hier hat 64 Zähne, das Zentralrad verbunden mit dem Motus hat 24 Zähne. Damit haben wir die Übersetzung -8/3. Das Zwischenrad hat dann 20 Zähne. Der rote Punkt am Rad dient zur Orientierung beim Drehen des Rades (der Zahnkranz ist ja mit dem Rad verbunden). Der zweite rote Punkt am Motus zeigt die Berührung mit dem Satellitenrad vor dem Schwingen. Das grüne Steuerpendel wird später vom Stampfwerk beeinflusst und moduliert damit die Geschwindigkeit des Motus.

Drehen wir jetzt das Rad cw bei freiem Steuerpendel, so wird sich beim Motus nichts ändern, da dieser ja Energie bräuchte um den Satelliten zu bewegen. Also dreht sich das Zwischenrad und lenkt dabei das Steuerpendel aus. Wir wollen aber doch den Satelliten starten und ihn möglichst schnell herumschwingen, also müssen wir den Hebel zurückdrehen, mit einer Mechanik vom Stampfer her.

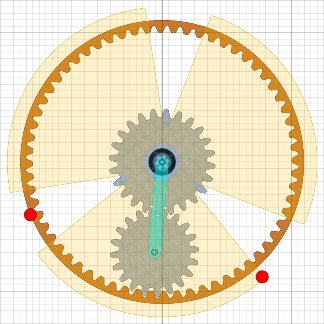Greift dann der Stampfer ein und eine geeignete Mechanik dreht das Pendel zurück, so dreht der Motus an und wird viel schneller als die 8/3-fache Geschwindigkeit des Rades. Der Satellit beschleunigt sehr schnell, die Feder wird gespannt und zum Ende der Umdrehung passt sich die Geschwindigkeit dem langsamen Einrasten des Fluggewichts an. Dazu muss die Zeitkonstante des Pendels natürlich gut mit der Drehzahl des Rades abgestimmt sein.

Bis hierher ist das Ganze recht überschaubar und läuft auch bidirektional.

Aber wie hat Bessler nur die Anregung des Steuerpendels gelöst?
Das bleibt immer noch sein Geheimnis.

nächste Seite: Ausblick