Die Zeit ist reif für den ersten Bauplan

Vom ersten Rad Besslers, das er am 6. Juni 1712 in Gera öffentlich präsentierte, ist wenig bekannt, nur der Durchmesser von etwa 5 Fuß (DT 107). Etwas mehr ist vom zweiten Rad von Draschwitz überliefert. Nach Aussage von Bessler war dieses wie das erste aufgebaut (DT 18), nur größer, 5 Ellen, also doppelt so groß im Durchmesser.

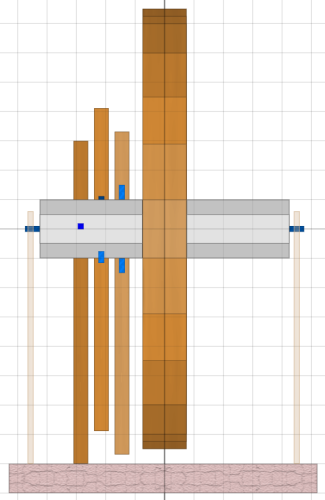
Hier im Bild ist also das erste Rad mit ca. 150 cm Durchmesser dargestellt. Dazu der Bericht von Gottfried Teuber (1656 - 1731), Zeitzer Hofdiakon und Magister, der darin das zweite Rad Besslers, das Draschwitz-Rad von 1714 beschrieben hat: „Es handelt sich um ein hohles Holzrad, 10 Fuß im Durchmesser und 6 Zoll dick. Es wird von dünnen Holzbrettern bedeckt, die den Mechanismus verbergen. Die Achse ist auch aus Holz und ragt auf beiden Seiten einen Fuß über das Rad hinaus. Sie hat Zähne, die 3 Stampfhölzer bewegen, ähnlich wie man sie in Stampfmühlen findet. Diese Stampfhölzer sind recht schwer, und sie werden unablässig angehoben und wieder fallen gelassen. Die eisernen Achszapfen drehen sich in offenen Lagern, so dass man einen Betrug durch äußere Energiezuführung ausschließen kann. Ich hatte mit dem Erfinder ein Treffen vereinbart. Als wir uns der Maschine näherten, konnte ich sehen, dass das Rad mit einem dicken Seil arretiert war. Sobald das Seil gelöst wurde, begann sich die Maschine mit großer Kraft zu drehen. Für längere Zeit hat sie ihr Tempo weder beschleunigt noch verlangsamt. Um sie wieder anzuhalten, war große Kraft erforderlich.” Das Bild hat ein Raster von 10 cm. Die Dicke des Rades beträgt ca. 16 cm, die Achse hat ca. 20 cm Durchmesser und die Stampfhölzer sind jeweils ca. 5 cm breit.

Das Äussere des Rades ist somit festgelegt, jetzt geht es an die „Eingeweide”, wie Bessler es auf den ersten Seiten seiner Apologischen Poësie nennt:
„Sein Eingeweyd’ gewinnt Gewicht/
  Sonst keine Uberwucht geschicht/”

Hier müssen bekannte und neue Prinzipien geschickt miteinander verbunden werden.
1) Die Unwuchterzeugung mit dem Scheren-Mechanismus ähnlich der früheren Seite „Wenn ein Pfund ..”;
2) die Anregung durch „fliehkraftfreie” Gewichte in der Achse, die gemäß MT34, MT69 (und auch MT40)
    für eine geeignete Vorspannung sorgen;
3) die an der richtigen Stelle eingebrachten Stampfer-Impulse, die die Ein- und Ausschwingvorgänge auslösen
    und sicher zum Abschluss bringen;
und 4) die MT18-Federn bei den ausschwingenden Fluggewichten.

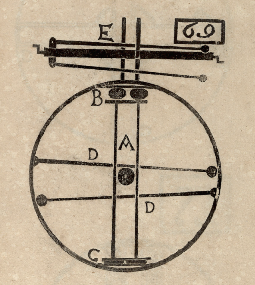
Um die Mechanik im Inneren der Achse zu verstehen schauen wir uns zunächst MT69 nochmal an. Für mich sind hier 3 Aspekte interessant: Zuerst die Hebel, die in der Achse liegen, mit Gewichten an den Enden. Dann die Darstellung wie die kleinen Auslenkungen der Hebel D im Rad eine Unwucht erzeugen und zum Dritten die Schreibweise der Zahl 69. Die Hebel D im Rad machen eigentlich wenig Sinn, wenn man die Fliehkraft berücksichtigt, ihre Reaktion zur Unwuchtverschiebung käme einfach zu spät. Geht man aber davon aus, dass die Hebel D identisch sind mit den Hebeln E, die fliehkraftfrei in der Achse liegen, dann ist auf einmal alles klar. Die Gewichte an den Enden der Hebel E sind so schwer, dass sie die Unwucht erzeugen können. Und ein Startimpuls, etwa an der Stelle wo das „E” steht, könnte die Bewegung zur richtigen Zeit auslösen (Stichwort Nockenwelle). (Bessler macht das sehr gerne, dass er die nicht sichtbare 3. Dimension durch eine 90 Grad-Drehung in die 2-dimensionale Darstellung bringt.) Jetzt wird auch klar wie MT40 zu interpretieren ist. MT40 zeigt nämlich die Anbindung des Scheren-Mechanismus an die Hebel in der Achse.

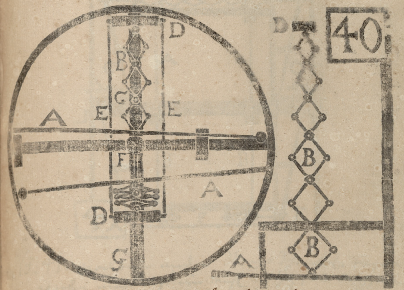
Wie bei MT69 sollte man sich die Hebel A in der Achse liegend vorstellen. Die Schere hat ihren Fixpunkt am Rad in C. Wird im oberen Bildteil das Scherenglied vom Hebel A nach unten gezogen, so wird das Gewicht D von den oberen Scheren-gliedern nach oben bewegt. Sehr interessant sind noch die zwei kleinen Rechtecke auf der waagerechten Speiche des Rades. Die naheliegende Interpretation ist natürlich, dass hier ein zweites System um 90 Grad versetzt arbeitet, dann würde das Rad sich im Gegenuhrzeigersinn drehen - auch interessant. Ich sehe im rechten Rechteck aber einen ganz kleinen Hinweis auf den Angriffspunkt eines Stampfers. Und damit kommen wir zum nächsten Bild, der technischen Umsetzung in einem Rad mit drei Stampfern.

Und da fangen die Darstellungsprobleme an:
Im Vergleich zum eigentlichen Rad sind die Dimensionen der Mechanik in der Achse winzig. Deshalb auch das Herausvergrößern in den folgenden Bildern. Auch die Übersetzungen der Kräfte sind beeindruckend.
Für mich ist Bessler „der Mann der irren Übersetzungen”. Und vielleicht ist gerade das sein Geheimnis.

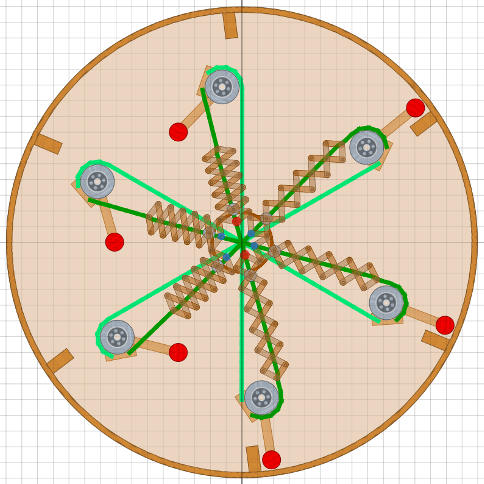
Hier endlich die Gesamtschau: Jeder Stampfer bedient eine Zapfenmechanik, also zwei Zapfen für zwei Scheren. Die Kunst Besslers war es, das alles in der Achse unterzubringen. Er konnte ja den Durchmesser nicht einfach vergrößern, da sonst zuviel Energie zum Heben der Stampfer notwendig geworden wäre.
In der Achse liegen 6 Hebel E (nach MT69), zwei rote (gerade aktiv) und vier blaue. In den verbleibenden Lücken muss die Mechanik der Zapfen Platz finden. Wenn das Rad sich im Uhrzeigersinn dreht und der Stampfer den Zapfen noch unten hält, wird der obere rote Punkt vom Hebel E um ca. 10 mm nach unten (=innen) gedrückt.

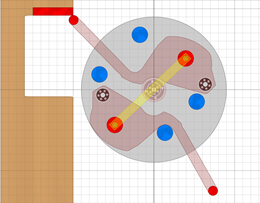
Zapfenmechanik vergrößert: 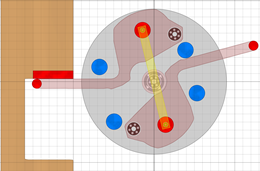Anfang Stampferhebung
Ende Stampferhebung ca.60 Grad Raddrehung pro Eingriff

Das Innenleben der Achse im Längsschnitt:

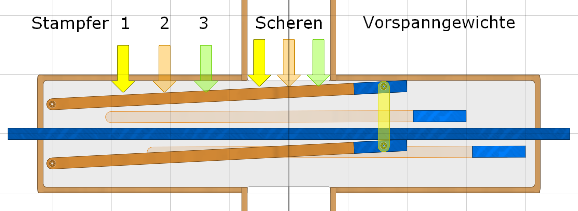
Im Inneren der Achse sehen wir eine durch-gehende Welle mit den Achszapfen an den Enden, die sich in den äusseren Lagern drehen (bei Bessler nur offene Pfannen) und sechs stabile Hebel, die die Stampferimpulse an die Scheren weiterleiten und am Ende jeweils schwere Gewichte haben.

Die Auslenkung von 10 mm beim Stampfer (z.B. gelber Pfeil 1) beträgt am Ansatzpunkt der Schere (gelber Pfeil im Zentrum des Rades) bereits mehr als 20 mm und der Scherenmechanismus macht daraus ca. 10 cm. Das reicht aus zum Ein- und Ausschwingen der Fluggewichte (nach MT138). Damit die beiden Hebel E parallel nach unten gehen, gibt es eine Kopplung der beiden (gelbe Verbindung), sie befindet sich bei den schweren Gewichten, den Vorspanngewichten. Die Vorspanngewichte müssen so schwer sein, dass sie fast alleine das Ein- und Ausschwingen der Fluggewichte durchführen könnten. Sie spannen die Scheren gerade so viel vor, dass sich noch nichts bewegt, aber dass es dann mit wenig Energie sehr schnell gehen kann, wenn der Stampfer eingreift.
An den Pfeilen sieht man, wo die Stampfer eingreifen und wo die Scheren ansetzen.
Wegen der geringen Dicke des Rades können die Abstände bei den drei Systemen nicht exakt gleich sein.
Vielleicht ist das der Grund, dass das Rad nicht ganz rund gelaufen ist (evtl. wie im Drei-Viertel-Takt).

Und jetzt verstehen wir auch den Vers Besslers in PA 29/30:
  „Alsbalde du versichert bist/
    Daß meine Welle nicht so ist/
    Sondern/ sie hat vielmehr viel Fächer/
    Ja durch und durch verschiedne Löcher.”

Die Welle war wohl nicht überall gleich dick und rund, sondern im Inneren wohl dicker, hatte aber da und dort Aussparungen, wo die Vorspanngewichte eintauchten und dort Löcher, wo die sechs Seile und die Verbindungen der Vorspanngewichte durchgingen.

Und jetzt noch kurz zur Zahl 69 in MT69 (siehe oben): Wie schon früher beschrieben: 6 + 9 = 15 - ein interessanter Aspekt. Aber auch die Schreibweise ist irgendwie besonders. Ich habe mal 6 und 9 vertauscht --- und sehe da den inneren Zapfenmechanismus.

Nachdem die einfachen Simulationsprogramme jetzt an ihre Grenzen kommen, bleibt uns nur noch der Versuch, der Bau eines Prototypen. Im Prinzip ist alles dargestellt und der Nachbau des Rades von Gera kann beginnen.

Dazu noch ein paar Hilfestellungen:
- die Drehzahl des Rades sollte zwischen 40 und 50 U/min liegen
- das Gewicht eines Stampfers beträgt wohl zwischen 6 und 10 kg
- ein Fluggewicht könnte ca. 0,5 bis 1,0 kg wiegen
- die Feder am Fluggewicht (MT18) muss zur Drehzahl passen (Federkonstante/Zeitkonstante)
- Zweit-Fluggewichte könnten die Anlaufeigenschaft und die Kraft des Rades verbessern
   (Zweit-Fluggewichte könnten zwischen den Haupt-Fluggewichten verbaut werden.
    Sie sind kleiner und werden von den Haupt-Fluggewichten verzögert nachgezogen,
    dadurch würde die Unwucht dann von 12 Massen erzeugt)
- zu guter Letzt sollte auch noch die Energie der fallenden Stampfer zurückgewonnen werden.

nächste Seite: Motus in 3D