MT18 mit zwei Armen

Die letzte Simulation scheint gut zu sein (fast so würde wohl Bessler reden), aber sie hat einen Nachteil: Es wäre keine durchgehende Welle durch das Bessler-Rad möglich - sehr unwahrscheinlich. Das Unwucht-Zahnrad muss also kleiner werden. Der Einfachheit wegen gehe ich mal von der halben Zähnezahl des äusseren Rades aus, das ist mit Tricks in der Praxis wohl machbar.

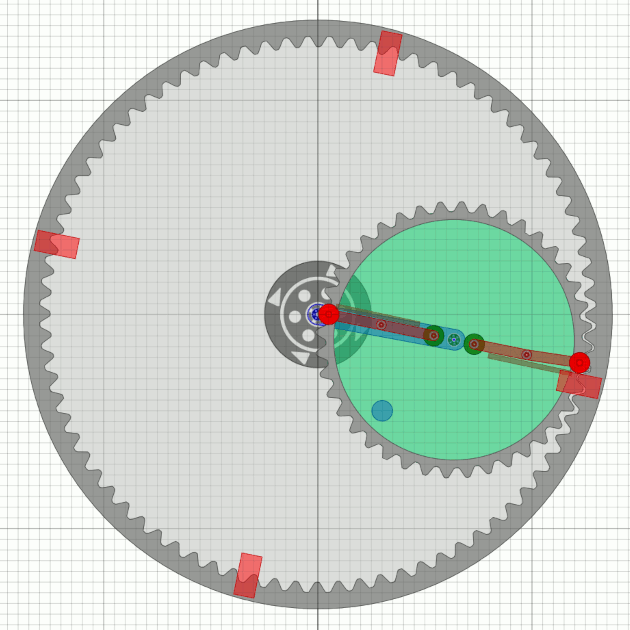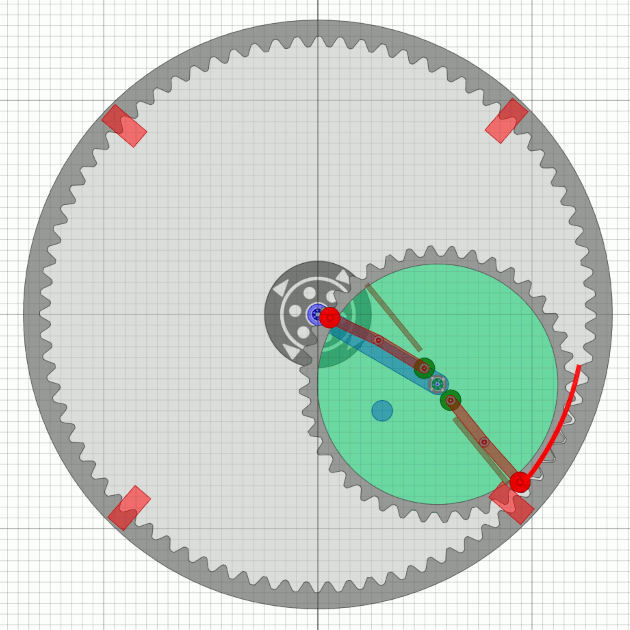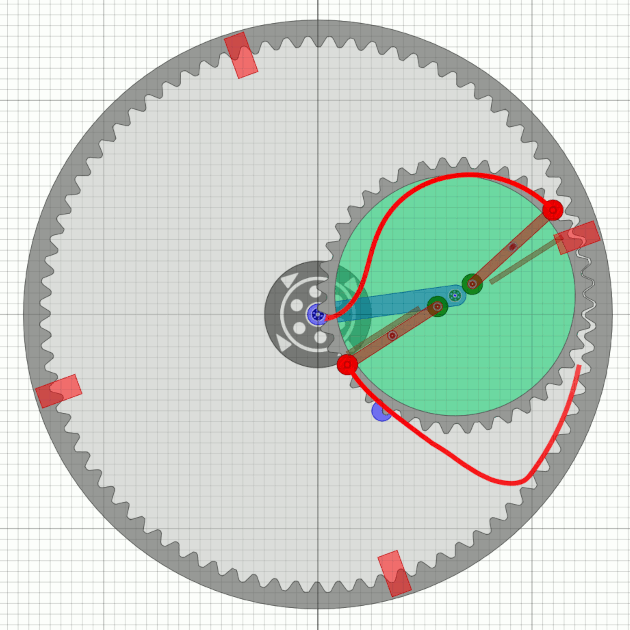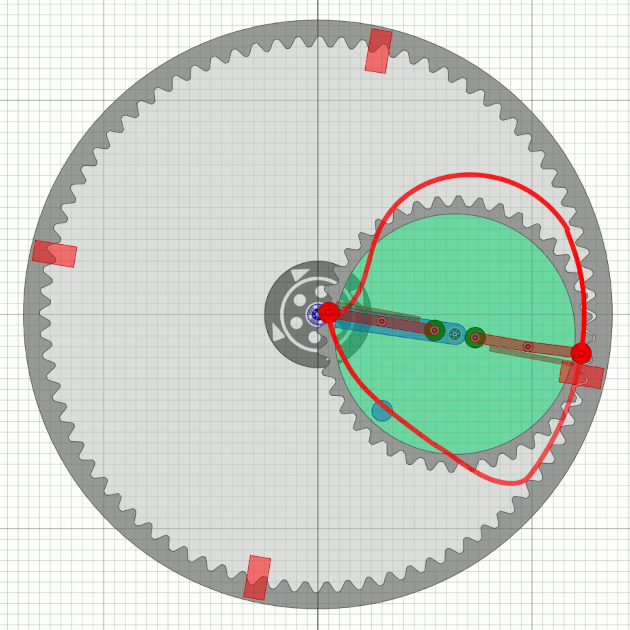
Ein Federarm arbeitet beim Hinausschwingen ähnlich einer Pendelschwingung und bestimmt mit seiner „Zeitkonstante” (Dimensionierung) die Drehzahl des Rades. Sowohl das Anheben als auch das Einrasten wird erleichtert und optimiert.

Wir sehen, dass es am Umfang vier Rastpunkte für die Fluggewichte geben muss. Mit der Annahme, dass ein zweites Unwucht-Zahnrad phasenversetzt läuft, gibt es dann 8 Rastpunkte.
Ist das vielleicht das Funktionsprinzip der letzten beiden Räder von Bessler?

Joseph Emanuel Fischer von Erlach (1693-1742) hat nach Besichtigung des Rades von Kassel berichtet:
  „... Bei jeder Drehung des Rades können vermutlich 8 Gewichte wahrgenommen werden,
    die jeweils auf der Seite nach unten fallen, nach der sich das Rad aktuell dreht.
    Es dreht sich mit erstaunlicher Geschwindigkeit, etwa 26 Umdrehungen pro Minute im Leerlauf.”

Bei der Animation ist zu berücksichtigen, dass sie um den Faktor 5 bis 6 verlangsamt ist. Die Abläufe sind in Wirklichkeit also viel schneller. Da braucht es schon einen kräftigen Anfangsimpuls um das Unwucht-Zahnrad zu heben (=> Stampfwerk).
Ich habe lange gebraucht bis ich einen Weg fand, die (Blatt-)Feder von MT18 mit Algodoo simulieren zu können. Dabei ist es ganz einfach: Mit dem Parameter „bend” im Lager kann man die Rotation ausschalten.
Das Lager wirkt dann wie eine Torsionsfeder mit einstellbarer Federkraft und einstellbarem Zielwinkel.
Dazu wird sehr wenig Rechenleistung benötigt und ich konnte mit 200 Hz simulieren.

Die Algodoo-Szene steht hier zum Download bereit, die script-Datei hier.

Und vielleicht sieht auch schon jemand einen Zusammenhang mit MT55.

nächste Seite: MT18 mit drei Armen