MT18 with two arms

The last simulation seems to be good (almost so Bessler would probably talk), but it has a disadvantage: There would be no continous shaft through the Bessler wheel possible - very unlikely. So the unbalance gear has to be smaller. For simplicity, I will assume half the number of teeth of the outer wheel, which is probably feasible with tricks in practice.

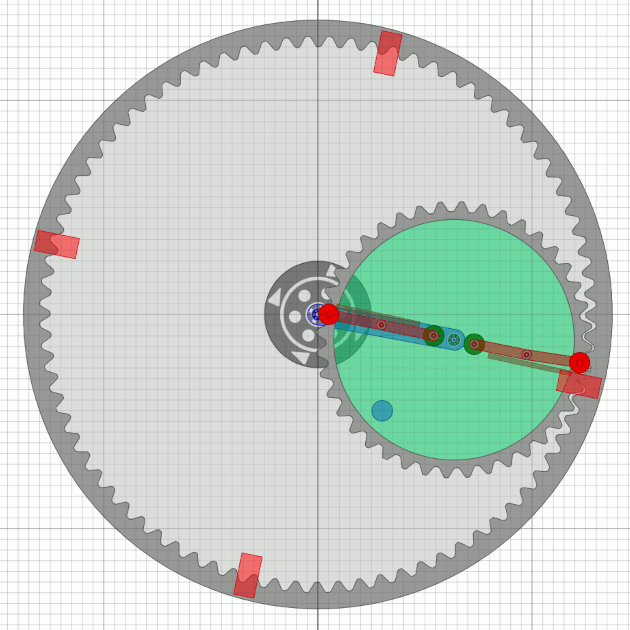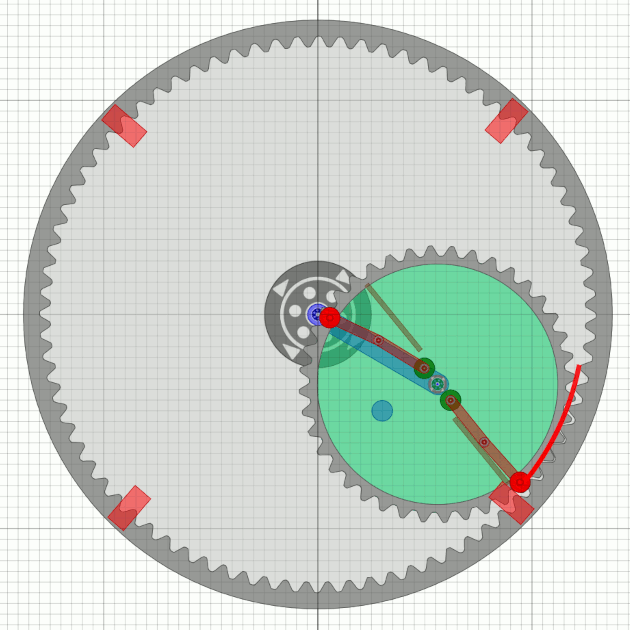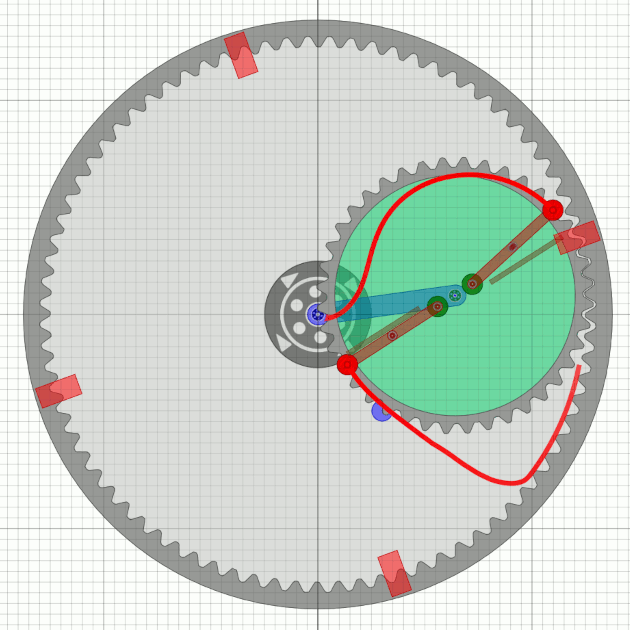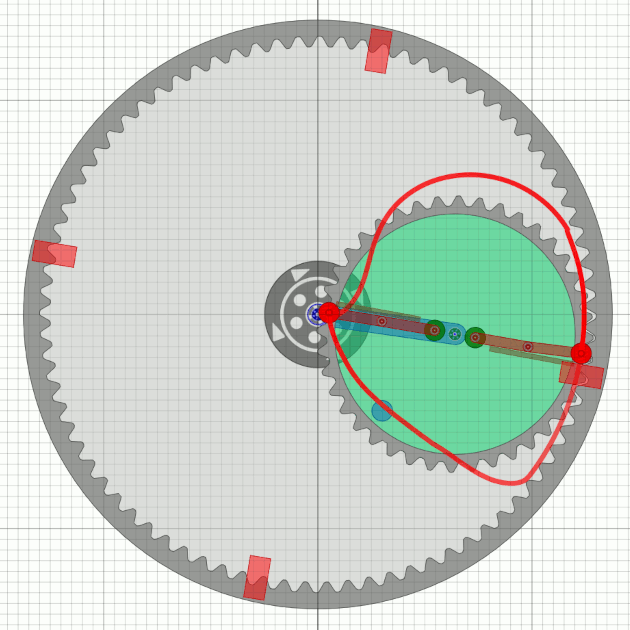When swinging out, a spring arm works in a similar way to a pendulum oscillation and determines the speed of the wheel with its „time constant” (dimensioning). Both lifting and arresting are facilitated and optimized.

We see that there must be four rest points on the circumference for the flying weights.
With the assumption that a second unbalance wheel runs phase-shifted, there are then 8 rest points.
Is this perhaps the operating principle of Bessler’s last wheels?

Joseph Emanuel Fischer von Erlach (1693-1742) reported after seeing the wheel of Kassel:
  „... With each rotation of the wheel probably 8 weights can be perceived,
    which fall down in each case on the side, after which the wheel turns at present.
    It turns at an amazing speed, about 26 revolutions per minute at idle.”

It should be taken into account that the animation is slowed by a factor of 5 to 6. The processes are therefore much faster in reality. A powerful initial impulse is needed to lift the unbalance gearwheel (=> stamper unit).
It took me a long time to find a way to simulate the (leaf) spring of MT18 with Algodoo. But now it’s quite simple:
With the parameter „bend” in a bearing you can make it not to rotate, but only be bent against a spring with adjustable parameters. This requires very little computing power and I was able to simulate with 200 Hz.

The Algodoo scene is available for download here, the script file here.

And maybe someone already sees a connection with MT55.

next page: MT18 with three arms