Die Steuerung im großen Rad

Bessler hat die Funktion seiner Räder bewusst verheimlicht. Trotzdem hat es ihn in den Fingern gejuckt und er hat in seinen Büchern immer wieder Hinweise eingestreut. In einer Verzierung auf jeder Seite des Hauptteils von Apologische Poesie hat er wohl die Steuerung der großen Räder an ganz prominenter Stelle dargestellt - als kleinen Stern in der Kopfzeile.

Was hier aussieht wie ein Stern, eine Verzierung, die die Seitenzahl einrahmt, ist in Wirklichkeit die abstrahierte Form der Steuerung im Bessler-Rad. Dieser Fund war für mich so eine kleine Bestätigung auf dem richtigen Weg zu sein.

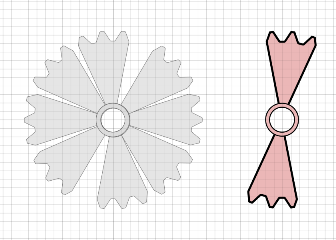
Wie früher dargestellt gibt es im Rad 2 x 5 Unwucht-Räder an 5 Balken (Doppelhebeln). Vier dieser Balken sind immer mit dem Rad verbunden (die Drehung der Unwucht-Räder ist blockiert), die Winkel zwischen ihnen bleiben konstant. Nur ein Balken ist frei und wird abgebremst. Er dreht sich dann relativ zum Rad rückwärts. Das abgebildete rosafarbene Teil ist ein Teilzahnrad, das jeweils mit einem Balken fest verbunden ist.

Wenn man zu vier Teilstücken das fünfte überlappend dazusetzt, hat man den Stern aus der Kopfzeile des Buches. Damit bei den fünf Balken jeweils zwei überlappen können, braucht es schon eine ausgeklügelte Mechanik. Das Teil darf nicht wie dargestellt durchgehend die anderen überlappen, sondern muss geteilt sein. Eine Seite gehört auf eine Seite des Rades (zu einem Motus) und die andere auf die andere Seite des Rades (zum zweiten Motus). Das untere Teil 5a müsste also real hinter Teil 1b liegen. Dargestellt ist hier eine 41,5 Grad Überlappung, die auch technisch realisierbar ist. Nur bei einer 45 Grad Überlappung würden sich aber genau 8 Takte pro Umdrehung ergeben (wie überliefert). Wie Bessler es genau gemacht hat wird sich noch zeigen.

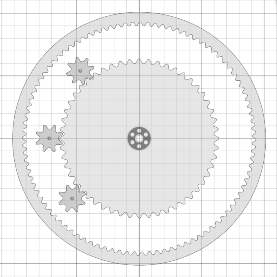
Hier sehen wir die Grundstruktur des Getriebes. Das große Rad hat aussen ein innenverzahntes Zahnrad. Das innere Zahnrad, Zentralrad oder Sonnenrad, ist mit diesem fest verbunden, dreht sich also mit gleicher Geschwindigkeit. Die drei kleinen Zahnräder links betrachten wir mal als ortsfest, sie drehen sich relativ schnell, wenn das Rad sich dreht. Legen wir jetzt ein Teilzahnrad hinein, dann ist dieses frei drehbar, solange es kein kleines Zahnrad berührt. Es dreht sich aber exakt mit dem Rad mit, wenn eines der kleinen Zahnräder eingreifen kann.

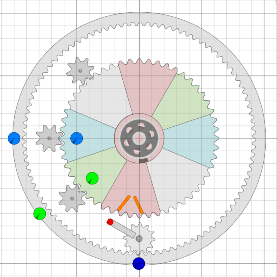
Statt fünf Teilzahnrädern sind hier mal drei eingelegt, rosa, grün und hellblau. Die grünen und blauen Orientierungspunkte drehen sich mit gleicher Winkelgeschwindigkeit, da die kleinen Zahnräder im Eingriff sind. Genau das wollen wir erreichen. Steht ein Teilzahnrad (rosa) dann fast senkrecht, so wird es von den kleinen Rädern freigegeben. Jetzt greift der kleine Hebel des Genfer-Rads unten in eine kleine Tasche ein und schwingt das Teilzahnrad und damit den Balken zurück, um etwa 45 Grad. Dabei drehen sich dann auch die Unwucht- oder Satellitenräder in der gewünschten Weise und die Gewichte schwingen ein bzw. aus. Angenommen ist hier eine Drehung des Rads im Uhrzeigersinn.

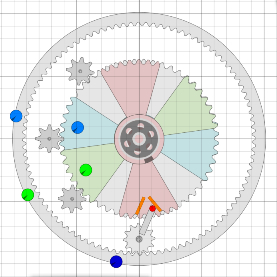
Hier hat sich das Rad ein paar Grad weitergedreht und das Zurückschwingen des Balkens ist schon fast abgeschlossen. Als nächstes wird das Teilzahnrad von einem kleinen Zahnrad erfasst und damit dreht der gesamte Balken sich wieder mit dem Rad. Man kann jetzt schon einen Eindruck bekommen wie schnell dieses Zurückschwingen eines Balkens abläuft und wieviel Energie dazu nötig ist. Die Energie kommt dabei aus vielen Quellen: einem Pendel, dem Stampfwerk und der Trägheit des Rades. Da es im Bessler-Rad kein „ortsfest” gibt, gehörten die kleinen Zahnrädern und das Genfer-Rad auch zu einem schwingenden System. Man kann sagen: Im Bessler-Rad war so ziemlich alles am Schwingen und hat sich gegenseitig aufgeschaukelt.

nächste Seite