Simulation

Wie bereits erwähnt benutze ich zur Simulation das kostenlose Programm Algodoo (Version V2.1.0). Dieses Programm ist gut geeignet für schnelle Tests mit wenigen Bauteilen, z.B. Pendel oder auch Getriebe. Probleme habe ich aber mit Ketten und Seilen oder wenn ich mehrere Teile auf dieselbe Welle positionieren muss. Auch Ratschen springen gerne über, evtl. weil Algodoo zu hohe Scherkräfte vermutet. Ein riesiger Vorteil der Simulation mit Algodoo ist, man bekommt schnell ein Gefühl für die Geschwindigkeit bzw. Drehzahl des Systems. Man sieht, dass 26 U/min schon sehr schnell ist und dass bei 50 U/min fast nur noch die Fliehkraft eine Rolle spielt.

Ich habe hier ein paar Beispiele zum Herunterladen eingestellt. Wer Algodoo auf seinem Rechner hat muss die heruntergeladene Datei nur in das Directory Algodoo/scenes einfügen und schon ist die Szene zum Testen verfügbar. Die Beispiele wurden auf einem Rechner mit 1600x900 erzeugt. Bei Rechnern mit geringerer Auflösung muss evtl. die Zoom-Funktion benutzt werden um einen geeigneten Bildausschnitt darstellen zu können.

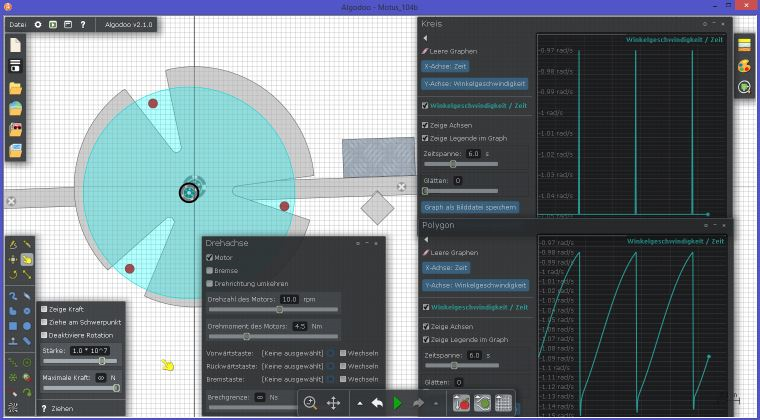
Mit obiger Szene Motus_104b kann man die Funktion des Motus testen. Das teiltransparente türkise Rad wird angetrieben und die angebrachten roten Zapfen greifen in den Motus ein. Drehzahl und Drehmoment können im Fenster unten Mitte eingestellt werden. Der Motus wird leicht gebremst. Die Fenster rechts zeigen die Winkelgeschwindigkeit des Antriebs (oben) und des Motus (unten). Die Spikes oben zeigen an wie die Drehzahl des Antriebs kurz einbricht, wenn ein Zapfen am Motus aufsetzt. Die Drehzahl wird dabei negativ angezeigt, weil Drehung im Uhrzeigersinn mathematisch (im kartesischen Koordinatensystem) negativ ist.
Das Antriebsrad hängt an einem Hebelsystem das anfangs blockiert ist. Zum Verschieben (Stichwort Winkel Ratschenwelle) müssen die Blockierungen am Balken entfernt werden und dann kann mit den Pfeiltasten die Auflage (gekipptes Quadrat) verschoben werden, wenn man es vorher per Mausklick anwählt. Ohne die Blockierung des Balkens wird die Sache sehr unruhig. Eine Verbesserung bringt die Beschwerung des Balkens durch den Stahlblock aber am besten fixiert man den Balken wieder nach dem Verschieben.

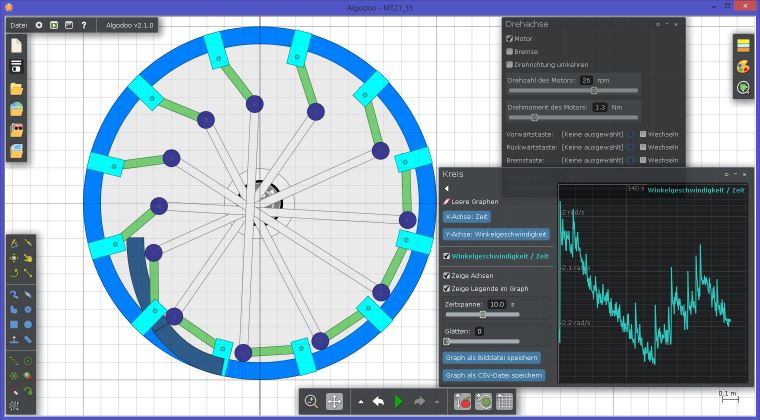
Die Szene MT21_33n zeigt das äussere System eines kleinen Rads mit hängenden Hebeln, ohne „Amboss”. Mit dieser Simulation kann man schön sehen wie schnell sich die Räder bewegt haben und wie sich dabei die Fliehkraft auswirkt. Der dunklere ortsfeste „Horizont” (nach oben enger werdende Bahn) eignet sich eigentlich gut zur Verschiebung der Fluggewichte mit wenig Energie. So eine Bahn wäre aber sicher überliefert worden. Wäre die Bahn im Rad gewesen (hierzu gibt es die Aussage eines Zeugen, der durch einen Spalt in der Bespannung von einer gekrümmte Bahn berichtet hat), dann müsste ein großes Gewicht (Pendel) die Ortsfestigkeit annähern. Das Rad wäre dann aber schwer geworden. Andererseits könnte die Auslenkung eines solchen Pendels auch zur „Ladung” der inneren Pendel genutzt werden.

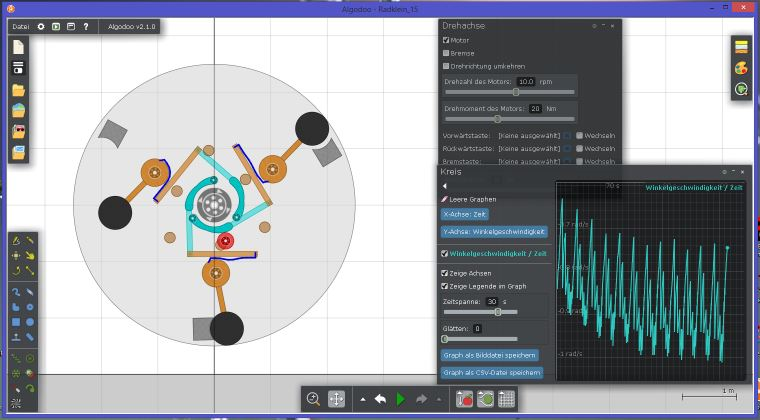
Diese Szene Radklein_15 zeigt das äussere Prinzip eines kleinen Rads wie Bessler es wohl verwendet hat. Bei der Simulation sieht man auch gut die Problematik mit Schnüren oder Seilen. Bessler war ja Spezialist von „irren” Übersetzungen und hat die Schnüre wohl mit zusätzlichen Federn in den Griff bekommen. Die Drehzahl darf man bei dieser Simulation nicht zu hoch treiben. Hier sieht man gut, dass man mit der Simulation eines kompletten Bessler-Rads sehr schnell an Grenzen kommt.

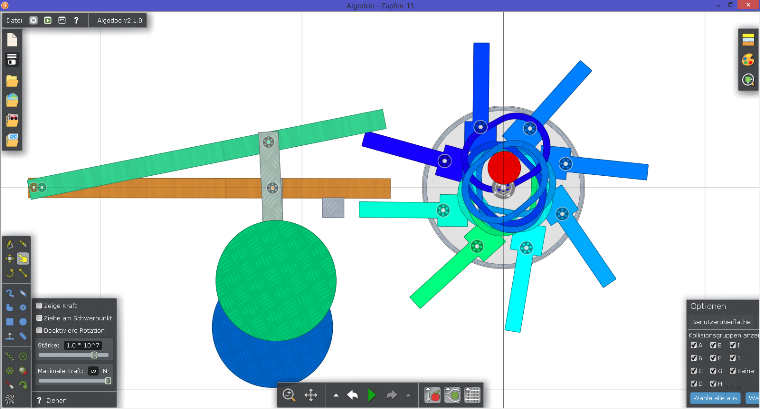
Die Szene Zapfen_13 skizziert das Prinzip der Anhebung der Ratschenwelle in der Achse. Dargestellt ist eine der ersten Simulationen mit Algodoo. Formen und Mechanik sind inzwischen natürlich verfeinert worden.

nächste Seite